二叉树初赛知识讲义

树和二叉树的定义

在了解二叉树的定义之前，我们必须先掌握树的定义。

树的定义

树（tree）是$n(n\geq 0)$个结点的有限集。在任意的一棵非空树中：

• 有且只有一个被称为根（root）的结点
• 当$n>1$时，除了根结点之外的结点可以分为$m(m>0)$个互不相交的有限集$T_1,T_2,\dots,T_m$，其中每一个集合又是一棵树，我们称它们为根结点的子树。

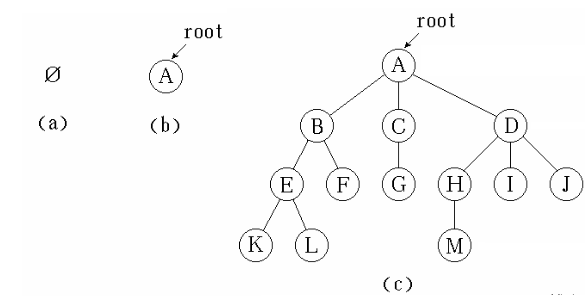
例如，上图中的(a)就不是一棵树，因为它没有根结点。而(b)则是一棵只有一个根结点的树。©就是一棵比较复杂的树了——它具有$13$个结点，其中$A$是树根，其余的结点被分为三个互不相交的子集:$T_1=\{B,E,F,K,L\},T_2=\{C,G\},T_3=\{D,H,I,J,M\}$。$T_1,T_2$和$T_3$都是根$A$的子树，且本身也是一棵树。

在根的子树中，依然存在子树。这里不再详细说明根的子树的子树的情况……大家需要知道的是，一直被分下去的子树最终只会是一个结点——到那个时候，也就不再存在子树的子树了。我们把没有子树的结点叫做叶子结点。

二叉树的定义

二叉树（binary tree)是另外一种树型结构。二叉树也是树，只不过比较特殊——二叉树的每个结点至多只有两棵子树。（即二叉树中不存在度大于二的结点），并且，二叉树的子树有左右之分，其次序是不可以随意颠倒的。

二叉树有下面的五种基本形态：

• 空树（即没有根结点的不相交有限集合，可以理解为什么都没有）
• 只有一个根结点的二叉树
• 有右子树的二叉树
• 有左子树的二叉树
• 左右子树都有的二叉树

树的相关术语也同样使用于二叉树。

树的表现方法

树的结果定义是一个递归的定义，即在树的定义中又运用到了树的概念，这蕴含了树固有的特性。（注意，这点将为日后写关于树的程序提供递归的理论依据）。其实，除了我们常见的结点表示法，树还有很多其他的表示方法，这里介绍两种。

括号表示法

比如下面的这颗树：

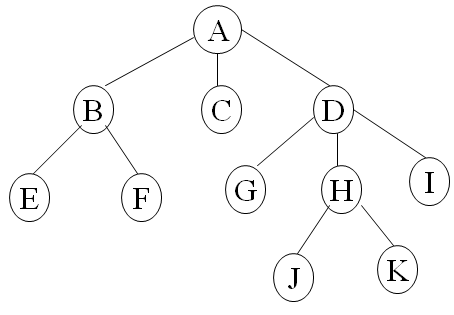
用括号表示法表示出来即为：A(B(E,F),C,D(G,H(J,K),I))

可以看出，所谓括号表示法只不过是把所有的子树层次给表示出来罢了。

维恩图表示法

依然以上面的树为例，用维恩图表示法表示出来的树大概长这样：

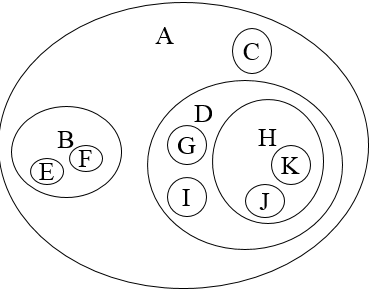
同样也是对子树的层次的描述。

树结构中的术语

树的结点包含一个数据元素和若干个指向其子树的分支。结点拥有的子树数称为结点的度（degree)。

例如，在树©中，$A$的度为$3$，$C$的度为$1$，$F$的度为$0$。度为$0$的结点称为叶子结点或终端节点（也有直接称其为“叶子”的）。在树©中，$K,L,F,G,M,I,J$都是树的叶子结点。相应地，度不为$0$的结点被称作是分支结点或非终端节点。除根结点外，分支结点也被称作是内部结点。树的度是树内各节点的度的最大值。树©的度为$3$。结点的子树叫做该结点的孩子(child)或后代或子孙（有时也叫后继），相应地，该结点称为孩子的父亲(parent)或祖先（有时也叫前驱）。例如，在树©中，$D$为$A$的子树$T_3$的根，则$D$是$A$的孩子，而$A$则是$D$的父亲。同一个父亲的孩子之间互称兄弟(sibling)。例如，在树©中，$H,I$和$J$互为兄弟。

结点的层次(level)从根结点定义起，根为第一层，根的孩子为第二层——若某结点在第$l$层，则其子树的根就在第$l+1$层。父亲在同一层的结点互为堂兄弟。例如，在树©中，$G$和$E,F,H,I,J$互为堂兄弟。树中结点的最大层称为树的深度(depth)或高度。树©的深度为$4$。

如果将树中结点的各子树看成从左至右是有次序的（即不能互换位置），则称该树为有序树，否则称其为无序树。在有序树中，最左边的子树的根称为树的第一个孩子，最右边的子树的根称为树的最后一个孩子。

森林(forest)是$m(m\geq0)$棵互不相交的树的集合。对数中每个结点而言，其子树的集合即为森林。由此，也可以用森林和数相互递归的定义来描述树。

就逻辑结构而言，任何一棵树都是一个二元组$T=(root,F)$，其中$root$是数据元素，称作是树的根结点；$F$是$m(m\geq0)$棵树的森林，$F=(T_1,T_2,\dots,T_m)$，其中$T_i=(r_i,F_i)$称作根$root$的第$i$棵子树；当$m\not=0$时，在树根和其子树森林之间就存在着下列关系：

$RF=\{<root,r_i>|i=1,2,\dots,m,m>0\}$

这个定义将有助于得到森林和树与二叉树之间转换的递归定义。

几种特殊的二叉树

满二叉树

一棵深度为$k$且有$2^k-1$个结点的二叉树被称为满二叉树(也叫作完美二叉树）。例如下面的这棵树就是一棵满二叉树：

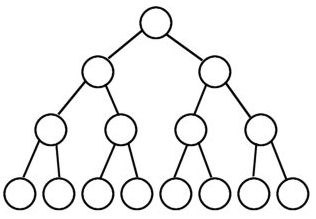
在满二叉树中的结点，要么是叶子结点（结点的度为 0），要么结点同时具有左右子树（结点的度为 2）.

完全二叉树

我们可以对满二叉树的结点进行连续编号，约定从根结点起，自上而下，自左至右。由此可以引出完全二叉树的定义。深度为$k​$的，有$n​$个结点的二叉树，当且仅当其每一个结点都与深度为$k​$的满二叉树一一对应时，称之为完全二叉树。完全二叉树除最后一层外的每层结点都完全填满，在最后一层上如果不是满的，则只缺少右边的若干结点。

什么意思呢？我们以下面的完全二叉树为例：

可以看到，完全二叉树的叶子结点分布在最后一层和倒数第二层。我们将完全二叉树的性质总结如下：

• 叶子结点只可能在可能在层次最大的两层上出现
• 对于任意的一个结点，若其右子树下的子孙的最大层次为$l$，则其左子树的最大层次必定为$l$或$l+1$

完全二叉树有许多重要的性质，将在下一节中介绍。

二叉树的性质

我们着重来讲一讲二叉树的性质。因为这方面是NOIP初赛的重点。

二叉树具有下列重要特性：

• 性质一 在二叉树的第$i$层上至多有$2^{i-1}$个结点$(i\geq0)$

  我们可以利用数学归纳法来证明此命题。

  当$i=1$时，只有一个根结点。显然，$2^{i-1}=2^0=1$是正确的。

  现在假设有一数$j(1\leq j<i)$，易得第$j$层上至多有$2^{i-1}$个结点。那么，可以证明$j=i$时命题也成立。

  由数学归纳法假设：第$i-1$层上至多有$2^{i-1}$个结点。由于二叉树的每个节点的度至多为二，故在第$i$层上的最大结点数为第$i-1$层的最大结点数的两倍。即$2\times2^{i-2}=2^{i-1}$。

• 性质二：深度为$k(k\geq1)$的二叉树至多有$2^k-1$个结点。

  由性质一可得，深度为$k$的二叉树的最大结点数为:

  $f(k)=\sum_{i=1}^k2^{i-1}=2^k-1$

• 性质三：对于任何一棵二叉树$T$，如果其叶子结点的个数为$n_0$，度为二的结点数为$n_2$，那么$n_0=n_2+1$

  我们设$n_1$为二叉树$T$中度为一的结点数。因为二叉树中所有结点的度均小于或等于二，因此二叉树$T$的结点总数为:

  $n=n_0+n_1+n_2$

  我们再来考虑二叉树中的分支数。除了根节点之外，其余的结点都有一个分支进入，设$B$为分支总数，则$n=B+1$。由于这些分支是度为一或二的结点射出的，所以又有$B=n_1+2n_2$。于是得：

  $n=n_1+2n_2+1$

  结合上述方程组，得：

  $n_0=n_2+1$

• 性质四：具有$n​$个结点的完全二叉树的深度为$\lfloor \log_2n\rfloor+1​$

  请确保理解了上一节中对完全二叉树的相关定义。

  假设完全二叉树$T$的深度为$k$，根据性质二和完全二叉树的定义有：

  $2^{k-1}-1<n\leq2^k-1​$或$2^{k-1}\leq n<2^k​$

  于是$k-1\leq \log_2n<k$

  因为$k>0$

  所以$k=\lfloor \log_2n\rfloor+1$。

• 性质五：如果对一棵有$n​$个结点的完全二叉树$T​$的结点按层序遍历编号，则对任一结点$i(1\leq i\leq n)​$，有：

  • 如果$i=1​$，则结点$i​$就是$T​$的根，没有父亲；如果$i>1​$，则其父亲的编号为$\lfloor \frac{i}{2}\rfloor​$。
  • 如果$2i>n$，则结点$i$没有左子树，即结点$i$是叶子结点。否则其左孩子的编号为$2i$
  • 如果$2i+1>n$，则结点$i$没有右子树；否则其右孩子的编号是$2i+1$

  对于上面的命题，这里不给出证明。但这不意味着它不重要。感兴趣的同学可以自行上网搜索。

二叉树的遍历

在二叉树的一些应用当中，我们经常需要对结点进行访问。这就提出了一个遍历二叉树(traversing binary tree)的问题，即如何按某条搜索路径寻访树中的每一个结点，使得每个结点都被访问一次，而且只被访问一次。“访问”是一个很广的含义，可以是对结点进行某种处理，也可以是打印结点的值，甚至是释放结点所占的内存空间。遍历对于线性结构来说是非常容易的，用$O(n)$的暴力做法就可以解决。但遍历二叉树则是一个相对困难的过程——我们需要整理出一种规律，以便使二叉树上的结点可以排列在一个线性结构上，从而便于遍历。

回顾二叉树的递归定义，我们知道二叉树是由三个基本单位组成：根结点，左子树和右子树。因此，我们若是可以一次遍历这三部分，那么我们就可以遍历整棵二叉树了。伟大的计算机科学家们为我们创造了如下的遍历算法：先序遍历，中序遍历和后序遍历。

先序遍历

先序遍历的定义为：

若二叉树为空，则为空操作，否则：

1. 访问根结点
2. 先序遍历左子树
3. 先序遍历右子树

中序遍历

中序遍历的定义为：

若二叉树为空，则为空操作，否则：

1. 中序遍历左子树
2. 访问根结点
3. 中序遍历右子树

后序遍历

后序遍历的定义为：

若二叉树为空，则为空操作，否则：

1. 后序遍历左子树
2. 后序遍历右子树
3. 访问根结点

请务必掌握上述的遍历算法

二叉树的一些应用

这里简单列举一例，不再赘述：

• 二叉树存储表达式（支持前缀、中缀、后缀表达式）

有兴趣的同学可以自行上网搜索相关资料。