使用了Java中的BigDecimal来进行高精度计算，下面是代码：（Java党的福利qwq）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

import java.util.Scanner;
import java.math.BigInteger;
import java.math.BigDecimal;
import java.text.DecimalFormat;
class Main {
    public static  void main(String[] args)throws Exception
    {
        Scanner input = new Scanner(System.in);
        while(input.hasNext())
        {
            BigDecimal a= input.nextBigDecimal();
            BigDecimal b=input.nextBigDecimal();
            BigDecimal c= a.add(b);
            BigDecimal d= c.stripTrailingZeros();
            String s;
            s=d.toPlainString();
            System.out.println(s);
        }
        input.close();
    }
}

这是一道很考验数学素质的一道题目。但是作为一名优秀每天划水的OIer，这道题是不难的。来看我的分析：

因为数字很大，因此我们可以求以$10$为底的对数:$lgv=lg(x^{M+1}-1)-(M+) \times lg2+(2^E-1) \times lg2=lgA+B$。

根据题意可以推算出最大值$v_max=(1-\frac{1}{2^{M+1} })\times 2^{ {2^E}-1}=A\times 10^B$。

然后我们遍历所有可能的$M$，根据上面推导出来的公式求$E$的值，然后再利用$E$和$M$求出$lgv$和输入的值进行比较，如果相等，说明$M$和$E$就是所求的值。做两个浮点数相等判断的时候，我们需要设置一个误差常量$eps$,具体大小要根据具体的题目来定。

完整的程序(c++11)如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

#include <bits/stdc++.h>
using namespace std;
const double EPS=1e-6;
int main(void)
{
	char line[256];
	double lg2=log10(2),a,v;
	int b;
	while(scanf("%s",line)==1&&strcmp(line,"0e0")!=0)
	{
		*strchr(line,'e')=' ';
		sscanf(line,"%lf%d",&a,&b);
		v=log10(a)+b;
		for(int m=1;m<=10;++m)
		{
			int mhe=round(log10((v+m*lg2-log10(pow(2,m)-1))/lg2+1)/lg2);
			if(fabs(((1<<mhe)-1)*lg2+log10(pow(2,m)-1)-m*lg2-v)<=EPS)
			{
				printf("%d %d\n",m-1,mhe);
				break;
			}
		}
	}
	return 0;
}

树和二叉树的定义

在了解二叉树的定义之前，我们必须先掌握树的定义。

树的定义

树（tree）是$n(n\geq 0)$个结点的有限集。在任意的一棵非空树中：

• 有且只有一个被称为根（root）的结点
• 当$n>1$时，除了根结点之外的结点可以分为$m(m>0)$个互不相交的有限集$T_1,T_2,\dots,T_m$，其中每一个集合又是一棵树，我们称它们为根结点的子树。

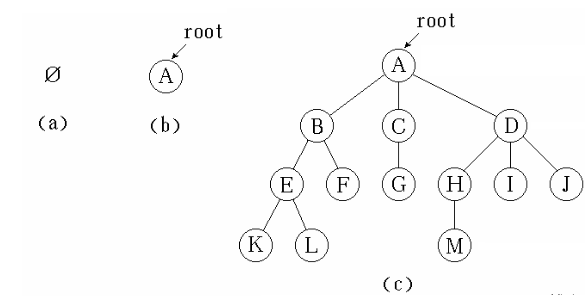
例如，上图中的(a)就不是一棵树，因为它没有根结点。而(b)则是一棵只有一个根结点的树。©就是一棵比较复杂的树了——它具有$13$个结点，其中$A$是树根，其余的结点被分为三个互不相交的子集:$T_1=\{B,E,F,K,L\},T_2=\{C,G\},T_3=\{D,H,I,J,M\}$。$T_1,T_2$和$T_3$都是根$A$的子树，且本身也是一棵树。

在根的子树中，依然存在子树。这里不再详细说明根的子树的子树的情况……大家需要知道的是，一直被分下去的子树最终只会是一个结点——到那个时候，也就不再存在子树的子树了。我们把没有子树的结点叫做叶子结点。

二叉树的定义

二叉树（binary tree)是另外一种树型结构。二叉树也是树，只不过比较特殊——二叉树的每个结点至多只有两棵子树。（即二叉树中不存在度大于二的结点），并且，二叉树的子树有左右之分，其次序是不可以随意颠倒的。

二叉树有下面的五种基本形态：

• 空树（即没有根结点的不相交有限集合，可以理解为什么都没有）
• 只有一个根结点的二叉树
• 有右子树的二叉树
• 有左子树的二叉树
• 左右子树都有的二叉树

树的相关术语也同样使用于二叉树。

树的表现方法

树的结果定义是一个递归的定义，即在树的定义中又运用到了树的概念，这蕴含了树固有的特性。（注意，这点将为日后写关于树的程序提供递归的理论依据）。其实，除了我们常见的结点表示法，树还有很多其他的表示方法，这里介绍两种。

括号表示法

比如下面的这颗树：

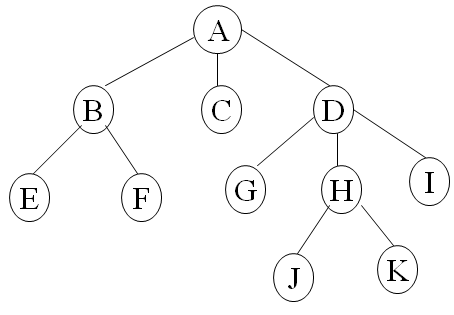
用括号表示法表示出来即为：A(B(E,F),C,D(G,H(J,K),I))

可以看出，所谓括号表示法只不过是把所有的子树层次给表示出来罢了。

维恩图表示法

依然以上面的树为例，用维恩图表示法表示出来的树大概长这样：

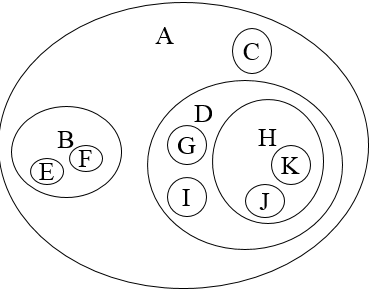
同样也是对子树的层次的描述。

树结构中的术语

树的结点包含一个数据元素和若干个指向其子树的分支。结点拥有的子树数称为结点的度（degree)。

例如，在树©中，$A$的度为$3$，$C$的度为$1$，$F$的度为$0$。度为$0$的结点称为叶子结点或终端节点（也有直接称其为“叶子”的）。在树©中，$K,L,F,G,M,I,J$都是树的叶子结点。相应地，度不为$0$的结点被称作是分支结点或非终端节点。除根结点外，分支结点也被称作是内部结点。树的度是树内各节点的度的最大值。树©的度为$3$。结点的子树叫做该结点的孩子(child)或后代或子孙（有时也叫后继），相应地，该结点称为孩子的父亲(parent)或祖先（有时也叫前驱）。例如，在树©中，$D$为$A$的子树$T_3$的根，则$D$是$A$的孩子，而$A$则是$D$的父亲。同一个父亲的孩子之间互称兄弟(sibling)。例如，在树©中，$H,I$和$J$互为兄弟。

结点的层次(level)从根结点定义起，根为第一层，根的孩子为第二层——若某结点在第$l$层，则其子树的根就在第$l+1$层。父亲在同一层的结点互为堂兄弟。例如，在树©中，$G$和$E,F,H,I,J$互为堂兄弟。树中结点的最大层称为树的深度(depth)或高度。树©的深度为$4$。

如果将树中结点的各子树看成从左至右是有次序的（即不能互换位置），则称该树为有序树，否则称其为无序树。在有序树中，最左边的子树的根称为树的第一个孩子，最右边的子树的根称为树的最后一个孩子。

森林(forest)是$m(m\geq0)$棵互不相交的树的集合。对数中每个结点而言，其子树的集合即为森林。由此，也可以用森林和数相互递归的定义来描述树。

就逻辑结构而言，任何一棵树都是一个二元组$T=(root,F)$，其中$root$是数据元素，称作是树的根结点；$F$是$m(m\geq0)$棵树的森林，$F=(T_1,T_2,\dots,T_m)$，其中$T_i=(r_i,F_i)$称作根$root$的第$i$棵子树；当$m\not=0$时，在树根和其子树森林之间就存在着下列关系：

$RF=\{<root,r_i>|i=1,2,\dots,m,m>0\}$

这个定义将有助于得到森林和树与二叉树之间转换的递归定义。

几种特殊的二叉树

满二叉树

一棵深度为$k$且有$2^k-1$个结点的二叉树被称为满二叉树(也叫作完美二叉树）。例如下面的这棵树就是一棵满二叉树：

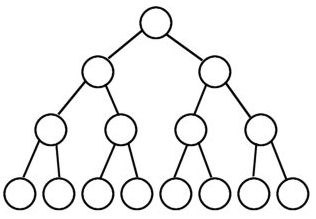
在满二叉树中的结点，要么是叶子结点（结点的度为 0），要么结点同时具有左右子树（结点的度为 2）.

完全二叉树

我们可以对满二叉树的结点进行连续编号，约定从根结点起，自上而下，自左至右。由此可以引出完全二叉树的定义。深度为$k​$的，有$n​$个结点的二叉树，当且仅当其每一个结点都与深度为$k​$的满二叉树一一对应时，称之为完全二叉树。完全二叉树除最后一层外的每层结点都完全填满，在最后一层上如果不是满的，则只缺少右边的若干结点。

什么意思呢？我们以下面的完全二叉树为例：

可以看到，完全二叉树的叶子结点分布在最后一层和倒数第二层。我们将完全二叉树的性质总结如下：

• 叶子结点只可能在可能在层次最大的两层上出现
• 对于任意的一个结点，若其右子树下的子孙的最大层次为$l$，则其左子树的最大层次必定为$l$或$l+1$

完全二叉树有许多重要的性质，将在下一节中介绍。

二叉树的性质

我们着重来讲一讲二叉树的性质。因为这方面是NOIP初赛的重点。

二叉树具有下列重要特性：

• 性质一 在二叉树的第$i$层上至多有$2^{i-1}$个结点$(i\geq0)$

  我们可以利用数学归纳法来证明此命题。

  当$i=1$时，只有一个根结点。显然，$2^{i-1}=2^0=1$是正确的。

  现在假设有一数$j(1\leq j<i)$，易得第$j$层上至多有$2^{i-1}$个结点。那么，可以证明$j=i$时命题也成立。

  由数学归纳法假设：第$i-1$层上至多有$2^{i-1}$个结点。由于二叉树的每个节点的度至多为二，故在第$i$层上的最大结点数为第$i-1$层的最大结点数的两倍。即$2\times2^{i-2}=2^{i-1}$。

• 性质二：深度为$k(k\geq1)$的二叉树至多有$2^k-1$个结点。

  由性质一可得，深度为$k$的二叉树的最大结点数为:

  $f(k)=\sum_{i=1}^k2^{i-1}=2^k-1$

• 性质三：对于任何一棵二叉树$T$，如果其叶子结点的个数为$n_0$，度为二的结点数为$n_2$，那么$n_0=n_2+1$

  我们设$n_1$为二叉树$T$中度为一的结点数。因为二叉树中所有结点的度均小于或等于二，因此二叉树$T$的结点总数为:

  $n=n_0+n_1+n_2$

  我们再来考虑二叉树中的分支数。除了根节点之外，其余的结点都有一个分支进入，设$B$为分支总数，则$n=B+1$。由于这些分支是度为一或二的结点射出的，所以又有$B=n_1+2n_2$。于是得：

  $n=n_1+2n_2+1$

  结合上述方程组，得：

  $n_0=n_2+1$

• 性质四：具有$n​$个结点的完全二叉树的深度为$\lfloor \log_2n\rfloor+1​$

  请确保理解了上一节中对完全二叉树的相关定义。

  假设完全二叉树$T$的深度为$k$，根据性质二和完全二叉树的定义有：

  $2^{k-1}-1<n\leq2^k-1​$或$2^{k-1}\leq n<2^k​$

  于是$k-1\leq \log_2n<k$

  因为$k>0$

  所以$k=\lfloor \log_2n\rfloor+1$。

• 性质五：如果对一棵有$n​$个结点的完全二叉树$T​$的结点按层序遍历编号，则对任一结点$i(1\leq i\leq n)​$，有：

  • 如果$i=1​$，则结点$i​$就是$T​$的根，没有父亲；如果$i>1​$，则其父亲的编号为$\lfloor \frac{i}{2}\rfloor​$。
  • 如果$2i>n$，则结点$i$没有左子树，即结点$i$是叶子结点。否则其左孩子的编号为$2i$
  • 如果$2i+1>n$，则结点$i$没有右子树；否则其右孩子的编号是$2i+1$

  对于上面的命题，这里不给出证明。但这不意味着它不重要。感兴趣的同学可以自行上网搜索。

二叉树的遍历

在二叉树的一些应用当中，我们经常需要对结点进行访问。这就提出了一个遍历二叉树(traversing binary tree)的问题，即如何按某条搜索路径寻访树中的每一个结点，使得每个结点都被访问一次，而且只被访问一次。“访问”是一个很广的含义，可以是对结点进行某种处理，也可以是打印结点的值，甚至是释放结点所占的内存空间。遍历对于线性结构来说是非常容易的，用$O(n)$的暴力做法就可以解决。但遍历二叉树则是一个相对困难的过程——我们需要整理出一种规律，以便使二叉树上的结点可以排列在一个线性结构上，从而便于遍历。

回顾二叉树的递归定义，我们知道二叉树是由三个基本单位组成：根结点，左子树和右子树。因此，我们若是可以一次遍历这三部分，那么我们就可以遍历整棵二叉树了。伟大的计算机科学家们为我们创造了如下的遍历算法：先序遍历，中序遍历和后序遍历。

先序遍历

先序遍历的定义为：

若二叉树为空，则为空操作，否则：

1. 访问根结点
2. 先序遍历左子树
3. 先序遍历右子树

中序遍历

中序遍历的定义为：

若二叉树为空，则为空操作，否则：

1. 中序遍历左子树
2. 访问根结点
3. 中序遍历右子树

后序遍历

后序遍历的定义为：

若二叉树为空，则为空操作，否则：

1. 后序遍历左子树
2. 后序遍历右子树
3. 访问根结点

请务必掌握上述的遍历算法

二叉树的一些应用

这里简单列举一例，不再赘述：

• 二叉树存储表达式（支持前缀、中缀、后缀表达式）

有兴趣的同学可以自行上网搜索相关资料。

第0章 前言

第一节 什么是OI

OI(Olympiad in Informatics,信息学奥林匹克竞赛)是一门新鲜的竞赛学科。它和和物理、数学等竞赛性质相同。OI也是高考中唯一没有的竞赛学科(虽然我认为以后会加入)。那么问题来了，我们为什么要学习OI呢？

学习OI，在很大程度上不是为了开发产品，但事实上，开发产品的时候往往离不开OI中所涉及的算法。所以，如果想将来做软件业务的同学也需要学习OI。那么，到底什么是算法竞赛，什么是算法呢？

算法(Algorithm)，是算法竞赛的核心。程序中充斥着算法，生活中充斥着算法，数学里也充斥着算法。我们用下面的例题来讲解一下算法的妙处。

给定一个正整数$n$，求$1^2+2^2+3^2+……+n^2$的值。

这道题，也许许多同学都会想到一个解法：暴力求解法。也就是，我把$n$的值带入到函数$y=f(n)=\sum_{k=1}^{n}k^2$之中，就可以得到结果。当然了，暴力求解法是最简单的算法，无论是人工手算还是电脑计算都很方便。但是，当$n=10^5$时，手算是一时半会儿算不出结果的。于是，我们就需要更高级的算法。

通过对数学公式的推导。我们可以得到$y=f(n)=\sum_{k=1}^{n}k^2=\frac{n(n+1)(2n+1)}{6}$。这样，哪怕$n$的值很大很大，我们都可以通过几步的乘除法运算即可求出答案。感兴趣的同学可以看一下平方和公式的推导过程：

前提条件:$a^2+b^2=a(a+b)-b(a-b)$

设$S=1^2+2^2+3^2+\dots+n^2$

$S=1(2-1)+2(3-1)+\dots+n(n+1-1)$

$S=1·2+2·3+\dots+n(n-1)-\frac{n(n+1)}{2}$

$∵\frac{n(n+1)}{2}=\frac{1}{3}[n(n+1)(n+2)-(n-1)n(n+1)]$

$∴S=\frac{1}{3}(1\times2\times3-0\times1\times2)+\frac{1}{3}(2\times3\times4-1\times2\times3)+\dots+\frac{1}{3}[n\times(n+1)\times(n+2)$

$-(n-1)\times n\times(n+1)]$

$∴S=\frac{n(n+1)(2n+1)}{6}$

看到了吧？这就是算法的伟大。这也给了我们一些启示：

• 优秀的算法可以帮助我们减少工作量
• OI与数学是密不可分的亲兄弟
• 公式不是无缘无故产生的，而是推导出来的！

具体衡量算法的优秀程度的知识会在后面详细讲解。大家现在需要知道的是，算法是有优劣之分的！

上面的那个例子，仅仅是对式子的恒等变形来优化常数。然而，在一般的算法设计中，我们还需要其他的算法设计策略。

学习OI的好处

当然，学习并积极地参加到OI中是有很大的好处的。我简单地列举几点：

• 锻炼思维，开拓视野。
• 有利于升学。
• 更高效率地使用电脑。
• 可以提升你的数学能力和英语能力。
• 现代的互联网公司在面试的时候更加爱考察程序员的算法素养。因此今天学习OI，对将来想在计算机行业就业的同学也是非常有帮助的。

第二节 和OI相关的赛事

OI虽然是是一门新起的奥林匹克事业，但是关于OI的国内外赛事是很多的。如果希望通过参加这些比赛来获得荣誉，了解这些比赛是非常有必要的。

NOIP

NOIP(National Olympiad in Informatics in Provinces，全国青少年信息学奥林匹克联赛)，旧称分区联赛，是一项由CCF(China Computer Federation，中国计算机学会)承办的全国统一的OI赛事。NOIP分初赛和复赛——初赛是地级市一级的，为笔试，复赛是省与直辖市一级的，为上机。初赛一般在每年十月中旬举行，而复赛一般在每年十一月举行。NOIP支持的语言有C语言，C++语言和Pascal语言(在2020年，NOIP将不再支持Pascal语言)。为了顺应时代发展的潮流，本套讲义将由C语言和C++语言作为程序描述语言。

NOIP分普及组和提高组。普及组的难度较低，面向广大的小学生和初中生；提高组的难度较高，面向广大的高中生。NOIP在初赛和复赛都设置了等级奖励制度，即一二三等奖颁奖制度。一般来说，进入复赛的资格就是初赛一等奖。不同的省的分数线一般都不一样，浙江江苏的分数线尤其高，因此浙江和江苏的OIer需要付出更大的努力才可以获得NOIP的成功。

NOI

**NOI(National Olympiad in Informatics，全国青少年信息学奥林匹克竞赛)**是NOIP的兄弟比赛，是一项由CCF(China Computer Federation，中国计算机学会)承办的全国统一的OI赛事。NOI是国内包括港澳在内的省级代表队最高水平的大赛，自1984年至2018年，在国内包括香港、澳门，已组织了33次竞赛活动。每年经各省选拔产生5名选手(其中至少有一名是女选手)，由中国计算机学会在计算机普及较好的城市组织进行比赛。这一竞赛记个人成绩，同时记团体总分。

NOI期间，举办同步夏令营和NOI网上同步赛，给那些程序设计爱好者和高手提供机会。为增加竞赛的竞争性、对抗性和趣味性以及可视化，NOI组织进行团体对抗赛，团体对抗赛实质上是程序对抗赛，其成绩纳入总分计算。

NOI将从正式选手中选出成绩前50名，作为中国国家集训队，集训队队员将获得清华北大的保送资格。

其他的OI赛事

其他比较著名的OI赛事还有APIO，CTSC，IOI等。感兴趣的同学可以自行上网搜索。

第三节 什么是OJ

我们来稍微的了解一下什么是OJ(Online Judge)。OJ是很好的在线OI学习平台，它的中文名字叫做在线测评系统。OJ上面有许多信息竞赛的习题，我们通过做这些习题来提升自我——最后到达一种神犇的境界。我们主要使用下面的几个OJ：

• 洛谷|计算机科学教育新生态
• 温州中学OJ
• 古老的无名OJ

我主要是想讲一些OJ上面的测评信息的含义：

关于OJ的信息还有很多，这里不再赘述。

第四节 讲义信息与声明

本讲义由浙江巨硬科技有限公司旗下的巨硬教育撰写。由巨硬教育教研组全体成员参与编写。

copyright：本讲义的全部内容在 CC BY-SA 4.0-署名-相同方式共享 4.0协议之条款下提供，附加条款亦可能应用。

第一章 基础语义

第一节 C语言的输出语句

所谓输入输出，就是在控制台中输入输出。什么是控制台呢？看：

这就是一个控制台。也就是我们常说的命令提示符。一般的程序的输入输出都在这里完成。

我们从最简单的一个程序开始:Hello,World!

这道题目的唯一要求就是输出一行Hello,World!。为了让程序实现输出文本这个功能，我们需要用到下面的C语言输出语句：

1

printf("Hello,World!");

但是，只有那么一条语句，程序是不可能通过编译的。完整的正确的程序如下：

1
2
3
4
5
6

#include<stdio.h>
int main(void)
{
    printf("Hello,world!");
    return 0;
}

上面的程序有很多大家暂时不理解的地方：我们暂时把这些当做是固定搭配来记忆，以后会详细解释。所以，我们总结出的C语言程序框架是：

1
2
3
4
5
6

#include<stdio.h>
int main(void)
{

    return 0;
}

我们把程序所要执行的语句写在return 0;和{之间——正像上面的程序一样。

暂时记不住程序结构也没关系，练习的次数多了，以后自然会记住的，不要着急。

现在你学会了C语言的输出语句了吗？如果答案是肯定的，那么恭喜你，你已经成为了一名程序员，并且已经教会电脑说话了！

课后习题

1. 输出5次“Hello，World！”。

第二节 C语言的变量类型以及标识符命名规则

变量与常量

什么是变量呢？变量就是指值的大小会改变的量。比如大家在玩游戏时人物的血量值——血量值是一直在更新的，不是恒定不变的，那么血量值就是变量。

我们也可以从数学函数的角度理解变量。如函数$y=f(x)=ax+b$。其中的$x$和$y$就是变量。当然咯，有变量就会有常量。顾名思义，常量就是那些值一直不变的量。比如上述函数中的$a$和$b$。他们是不会变化的。

变量和常量的概念同样适合于C语言——或者说，它适用于所有的编程语言。

由于变量和常量里面存的是数值，所以我们就需要知道有哪些类型的数值：

• 整数
• 小数(浮点数)

在C语言中，同样有对应数值类型存储的变量(常量)的类型。如下表所示：

注：本表中所提供的精度范围只适用于$32$位的计算机。

这张表格很重要。我希望你们都可以把他给记住。我们来详细地读一下这张表。里面出现了一个新词：关键字。什么是关键字呢？关键字(也叫关键词)是一个语言的重要组成部分——他们非常特殊，因为他们对于语言语法的描述有至关重要的作用！

我们来看一些变量的定义语法:

1

int n;

我们首先写出了一个关键字int。之后是一个空格，空格后边是一个标识符——变量的名字。那么标识符的命名有什么样的规则呢？

标识符命名规则

标识符，通俗地讲，就是名字。我在这里讲一下标识符的命名规则：标识符可以包含英语的26个字母的大小写，也可以包含十个阿拉伯数字(但是不能是标识符的开头)，也可以包括下划线(_)，标识符不能是关键字，也不能拥有除上述字符之外的任何字符！！！。

比如说，下面的这些标识符就是不合法的：

• int
• 9years
• @59hahaha

第一个标识符错在哪里呢？标识符不能是关键字，而int是一个关键字。

第二个标识符错在哪里呢？标识符不可以以数字开头，而9是一个数字。

第三个标识符错在哪里呢？标识符不可以包含其他字符，而@是其他字符。

我再举几个合法的标识符的例子：

• C_Programming_Language
• year2018
• Macrohard
• _

第四个标识符是不是很出乎你的意料？

但是，我们通常有一套标识符的命名习惯：**标识符最好以小写字母开头，而不是其他。中间最好不要有阿拉伯数字(末尾可以)，单词和单词中间最好以下划线分割——否则从第二个单词起，单词的首字母大写。**我举几个正确的例子：

• hello_macrohard
• helloMacrohard
• macrohard365

合理的遵守标识符的命名规则有助于让你的代码更加优美。

课后习题

1. 口述C语言的标识符定义规则

第三节 C语言的输入语句

整型输入

我们对于一个人是否是文盲的评判标准是什么？他是否正确地能读和写。现在，我们已经让计算机学会了写，是时候让它学会读了。

我们从一个最简单的程序开始：a+b问题

1
2
3
4
5
6
7
8

#include<stdio.h>
int main(void)
{
    int a,b;
    scanf("%d%d",&a,&b);
    printf("%d",a+b);
    return 0;
}

上面的程序出现了一个之前从来都没有涉及到的语句：scanf语句：

1

scanf("%d%d",&a,&b);

上述代码的意义就是：从控制台读入两个整数，分别存放在变量$a$和$b$中。也就是说，假如我在控制台里边输入:

1

1 2

那么变量$a$和$b$的值将会是$1$和$2$。懂了吗？读入整数的规则就是这样的。我把它总结一下，总结在这里：

1

scanf("%d...",&?,&?,...&?);

假设我们要输入$n$个整数，变量的名字分别是$a1,a2,\dots,an$。那么我们就可以这样输入：

1

scanf("%d%d……%d",&a1,&a2,……,&an);

注意：输入整数的提示符是%d。逗号后面变量名字前面的&符号是必须的。我举几个错误的例子：

1

scanf("%D",&a);

1

scanf("%d",a);

第一个输入语句错在提示符错误。输入整数的提示符应该是%d，而不是%D。C语言是区分大小写的。

第二个输入语句错在变量前面没有加&符号。目前，我们所写的一切scanf语句都是需要&的。&是取地址操作。

上面的程序中的printf语句也有了新的用法：

1

printf("Hello,world!");

1

printf("%d",a+b);

看出区别了吗？第一个printf语句只拥有一个参数，而第二个拥有两个！不过，我们已经学习了scanf的用法，第二条printf语句的用法也是可以望文生义的。它的作用是：输出表达式$a+b$的值。

所以，对于执行两个整数的加法运算，这个程序像是天衣无缝了。但是，现实生活中，相加的两个数往往是实数，如何实现对实数的输入输出呢？

浮点输入

在上一节中，我们了解到：C语言中的变量(常量)的数值类型包含整型和浮点型。我在这里补充一点：浮点型变量也是可以存储整数的。如果想要让我们的程序支持浮点加法运算，我们首先需要把变量$a$和$b$改成浮点型的：

1

float a,b;

没错，那么接下来我们尝试着修改scanf语句。在上文我讲过：%d是输入输出整数的提示符，那么自然也有给小数准备的提示符，他是%f。

那么我们就可以把scanf语句修改成这样：

1

scanf("%f%f",&a,&b);

下面的printf语句也是一样的改法，完整的程序如下：

1
2
3
4
5
6
7
8

#include<stdio.h>
int main(void)
{
    float a,b;
    scanf("%f%f",&a,&b);
    printf("%f",a+b);
    return 0;
}

程序运行效果如下所示：

输出回车

结果没有任何问题。但是这个“请按任意键继续”出现在这里是不是有点难受？我们只需要在printf语句中做一个小小的变动即可：

1

printf("%f\n",a+b);

看到了吗？只需要加一个\n即可。在输出语句中，\n意味着输出一个回车。效果如下：

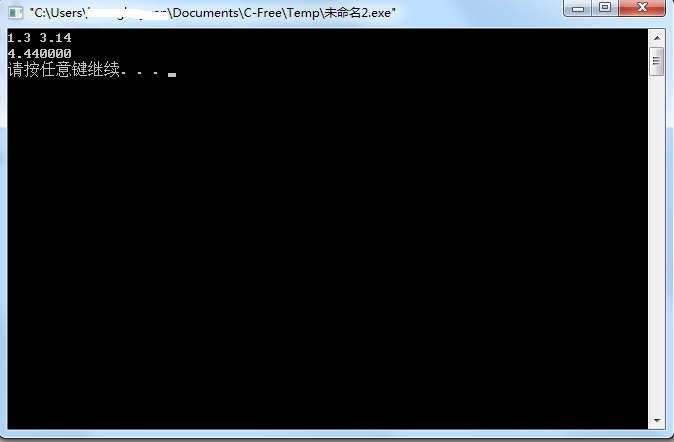
注意事项：在许多OJ中测评，有没有行尾回车都是无所谓的(也就是过滤多余的回车和空格)。但是也有一些严格的OJ，每一个空格和回车都会算的清清楚楚。所以，在做题的时候，输出一个行尾回车总是保险的。

现在你学会了输入语句了吗？恭喜你，现在你已经可以使用C语言进行简单的编程了！稍微总结一下提示符的用法：整数用%d，浮点数用%f。

课后习题

1. 请你完成这样的一个程序：此程序从控制台读入两个实数，输出它们的乘积。
2. 请你完成这样的一个程序：此程序从控制台读入一个整数和一个实数，输出它们的和。

第四节 C语言中的特殊符号的意义

空格在C语言中的意义

空格是什么？在我们的日常交流当中，空格没有任何的意义。比如这句话：“我 喜欢 C 语言 编 程 。”虽然字与字之间有一些空格，但我们还是可以读懂的。C语言也大致如此：只要不在标识符内部出现空格，其他部分出现空格一般是无害的。比如下面的这个程序：

1
2
3
4
5
6

#include    <stdio.h>
int                                  main       (   void    )
{
    printf        (      "Hello,world\n"      );
    return             0       ;
}

这个程序是完全正确的。可见，C语言编译器也和我们人一样，对空格不怎么敏感。

需要注意的是，TAB和回车的性质和空格相似，在此不再赘述。

注释

单行注释

什么是注释？我们来看一下注释的定义：

注释，是对书籍或文章的语汇、内容、背景、引文作介绍、评议的文字。为古书注释开始于先秦时期。中国古代分得较细，分别称之为注、释、传、笺、疏、章句等。包含的内容很广。诸凡字词音义、时间地点、人物事迹、典故出处、时代背景都是注释对象。有脚注、篇末注、夹注等形式。古籍注释列在正文之中，有双行夹注和夹注。现代书籍注释列于正文当页之下，称脚注，亦称本面注；列于文章之后或列于书籍之后者称篇末注。不管采用何种方式，全书注文的编排一般要求统一，以便于读者查考。注释在教科书中应用广泛，是学生学习的重要条件。

现代学术作品中的注释一般分内容解释和来源解释两种。前者多指对文章或书籍中某一部分词句作进一步说明，但为了防止冗杂而把它放在段落之外（文末或页边）。后者一般是为了保障原作者的著作权，注明某此语句、词语、观点的来源，以便读者的查证，另一方面也是为了尊重他人的知识产权和劳动。

那么注释在程序里面有什么用呢？很显然，注释的加入可以让人们充分的理解程序的意义。比如：

1
2
3
4
5
6

#include <stdio.h>
int main(void)
{
    printf("Hello,World!\n");//输出Hello,World!
    return 0;
}

上面的程序使用了C语言的单行注释的语法。拥有详细注释的程序对于初学者（甚至是根本不懂C语言的人）来说是非常友好的。因为他们可以通过注释中的内容来猜测出程序的作用。

单行注释由//打头//后边就是注释的内容。需要注意的是，单行注释是不可以跨行的。比如下面的程序就不是合法的：

1
2
3
4
5
6
7

#include <stdio.h>
int main(void)
{
    printf("Hello,World!\n");//输出
    Hello,World!
    return 0;
}

请记住这个规则，因为在很多编程语言当中，//都是单行注释的标志。

编译器对于任何的注释内容都是不会理会 。

跨行注释

跨行注释在C语言中的写法：

1
2
3

/*
这里写注释内容
*/

我需要说明很重要的一点：**跨行注释是不可以嵌套的！**比如下面的程序就不是合法的：

1
2
3
4
5
6
7
8
9
10

#include <stdio.h>
int main(void)
{
    printf("Hello,World!\n");
    /*
    输出
    /*Hello,World!*/
    */
    return 0;
}

基本运算符

我们知道，计算机的本职工作是做计算。那么在计算机中有哪一些常用的基本运算符呢？

加减乘除

在日常生活中，加减乘除运算应该是使用最频繁的运算了。C语言也提供了丰富的加减乘除运算的服务。符号表如下：

需要说明的是：**运算在C语言中同样存在优先级的问题。且乘除法运算的优先级比加减法大。**对于运算，我们有下面的运算规则：

先算优先级大的运算，再算优先级小的运算。总体顺序都是从左到右的。

注意：**在C语言中处理加减乘除运算时，符号两边要是都是整数，那结果就是整数如果有一个浮点数，则结果将是浮点数。**所以，这个表达式在C语言中的结果是3。但是如果是表达式或，结果就为想一想，为什么？

括号

当然，在C语言中，你也可以给运算加上括号，以此提升运算的优先级。需要说明的是：**C语言中只有小括号一种表示优先运算的括号！但是小括号也是可以嵌套的。**比如：$(1+(1+9))\times10-8$，在C语言中，这个算式是正确的。它对应着数学中的这个算式:$[1+(1+9)]\times10-8$。

取模运算

取模运算应该是大家从来都没有见过的。其实这个运算小学老师应该需要和大家讲——遗憾的是，取模运算一般在高等数学中才会学到。

我们先来观察一个算式：$10\div3=3\dots1$

还记得各个部分分别叫什么名字吗？$10$是被除数，第一个$3$是除数，第二个$3$是商，$1$是余数。我们的取模运算求的就是这个余数。比方说我们想要知道$2018$除以$365$的余数，在数学中，我们这样表示：$2018\,mod\,365$。在C语言中，我们这样表示：2018%365。%在C语言中就表达了取模运算的意思。

注意：取模运算的两个运算数一定要是int型的整型变量。

取模运算的优先级和乘除法同级。

课后习题

1. 请为自己编写的一个程序加上注释，要求使用单行注释和跨行注释。
2. 请把下面的表达式转化成C语言的表达形式：
   • $[1.5\times a+(\frac bc)]\times(a\,mod\,b)$
   • $2018\div365+\frac53$

第五节 输入输出语句扩展与字符变量

我们现在已经掌握了printf和scanf的基本使用方法：包括输入输出整型或浮点型的变量值。事实上，C语言还提供了其他的输入输出函数。

puts

puts函数的发明可谓是一个伟大的功绩。puts函数主要用于输出一个字符串——而不是输出变量的值。而且，puts函数输出字符串的时候自动输出一个回车。这些都不是重点，重点是：puts函数比printf快。

比如这个程序段：

1

printf("Hello,Macrohard!\n");

就可以等价于：

1

puts("Hello,Macrohard!");

如果大家在以后需要输出一个带回车的字符串，请使用puts来完成任务，毕竟这是一个优化的方法。

putchar

putchar是一个非常非常快速的输出函数。需要注意的是，putchar只能输出一个字符。使用方法如下:

1

putchar('?');//?是你需要输出的字符

注意：C语言里面字符串需要用一对双引号配合表达，而单个字符则使用单引号。

字符型变量

这里需要解释一下什么是字符型变量。字符型变量就是存储一个字符(注意，本讲义中的字符均指西文字符，而不是中文或其他字符)。

实际上，我们在计算机中是无法直接表示出一个字符的。所以我们需要借助ASCLL码表来存储一个字符。现代计算机科学存储字符的思路很明确：将字符标号，然后使用这个编号来表示字符即可。事实上，这世界上所有的主流的码表都是这样设计的。我们来看一下ASCLL码表的编码规则：

注：第128～255号为扩展字符（不常用）。

上表中出现了一个新的名词：转义字符。什么是转义字符呢？转义字符可以轻松地表达那些不便表达的字符——比如我们之前学的\n。转义字符都由\打头。

我需要说明的是：在C语言内部，字符类型其实是以整数的形式存储的。也就是说，char其实也是一种整型类型。

getchar

讲完了字符变量，也就可以讲getchar了。getchar函数的工作就是从控制台读取一个字符。比如下面的代码段:

1

printf("ASCALL码是:%d\n",getchar());

这个程序简单地讲述了一下getchar的用法。请牢记getchar的用法，这个函数在未来的程序编写中将由非常巨大的作用。

课后习题

1. 请你完成这样的一个程序：此程序从控制台读入一个字符，输出它的ASCLL码。
2. 请你完成这样的一个程序：此程序从控制台读入一个字符，请输出这个字符。

第六节 章节小结

到目前为止，我们已经讲完了C语言最基础的一部分语法。通过对这些输入输出函数的合理利用，相信大家已经可以完成一些非常简单的程序了。