已知,求的最大值
求的偏导数:
由费马定理,联立方程组:
解得:
故。故有最大值。
在初中阶段,往往不需要考虑多元函数是否有最值,但在后期的学习中却往往需要考虑。
传统的方法:
当且仅当,时,不等式取等号。故有最大值。
已知,求的最大值
求的偏导数:
由费马定理,联立方程组:
解得:
故。故有最大值。
在初中阶段,往往不需要考虑多元函数是否有最值,但在后期的学习中却往往需要考虑。
传统的方法:
当且仅当,时,不等式取等号。故有最大值。
平太给大介出了一道计算题(,各代表两位数中各位上的数字,相同的字母代表相同的数字):
大介:“得数是。”
平太:“不对。”
大介:“个位的数字对吗?”
平太:“对。”
大介:“其他数位的数字有对的吗?”
平太:“这是保密的。但你调换一下四位数中个数的位置,就能得出正确答案。”
请求出正确答案。
(第届日本数学奥林匹克决赛)
因为个位数为,所以只能是:
一一带入检验,得:
注意到只有与的构成数字完全相同。
故正确答案为。
已知点,为轴正半轴上一点,且满足,则点的坐标为?
(乐清六校理科班第一次联考,5018.9.28)
在平面直角坐标系中,设,,:
由三角函数的诱导公式知:
因为点在轴正半轴上,舍去。
故。
在中,有:
记,则:
故在上恒成立。
从而,在上为凸函数。
由琴生不等式得:
故
文本来源:鲁杰峰,马文杰:《论“数学抽象”的基本特征》[J].数学通讯(下半月),2019(1)
文中的<>中的文字是笔者加的。
数学抽象的基本特征
2.数学抽象具有客观性
数学是以抽象的方式与形式来反映客观世界的数量关系与空间形式的一门科学,具有一定的客观性。数学抽象的客观性常常表现为许多抽象的数学理论具有一定的客观现实背景,或者数学抽象的产物(即数学理论)在社会生活、科学研究中具有广泛的用途。《全日制义务教育数学课程标准(试验稿)》指出:“数学是人们对客观世界定性把握和定量刻画、逐渐抽象概括、形成方法和理论,并进行广泛应用的过程。”从本源上来说,很多数学概念或者数学理论是从现实世界客观存在的事物中,经过抽象,概括出客观事物之间的数量和数量的关系、图形与图形的关系。其数学抽象的过程并不是由人们凭空捏造、任意想象的,并不会因为某一个(类)人的某种观念的变化而发生改变。<参考欧根·杜林先生的数学先验论>数学抽象的客观性还表现在数学抽象的对象与结果是客观的。数学对象并不是没有内容的,也不是与现实世界毫无关系的,从本源上来说,许多数学对象来自于现实世界。在某一数学对象及其理论被数学家创造出来之后,就像现实世界客观存在的事物一样具有一定的客观属性。<不是观念!>另一方面,表现为数学概念,数学理论等的数学抽象的产物,其所蕴含的数学内容是有与其数学基础与逻辑保障的,并不断受到数学共同体的检验<实践是检验真理的唯一标准!>从这个角度而言,数学抽象具有一定的客观性。
已知,求证:
(命题)
求证:(命题)
使用第一数学归纳法进行证明:
当时,命题显然成立。
设当时,命题成立,即:
当时,有:
观察,得到:
同理也可以证明:
贝努利不等式是数学中十分重要的不等式:
其中,非零实数均大于且同号。
证明:使用第一数学归纳法进行证明:
当时:
考察不等式左边:
考察不等式右边:
因为,所以当时,不等式成立。
设当时不等式成立,即:
当时:
因为所以有:
因此,当时,命题成立。
综上,不等式获证。
求证:
(命题)
先证明一个引理(命题):
方程的根是:
注意到:
再证明一个基本的三角恒等式(命题):
由上一个引理:
令,则有:
现在证明原命题:
由三角恒等式得:
考察等式右边:
因为,所以命题得证。
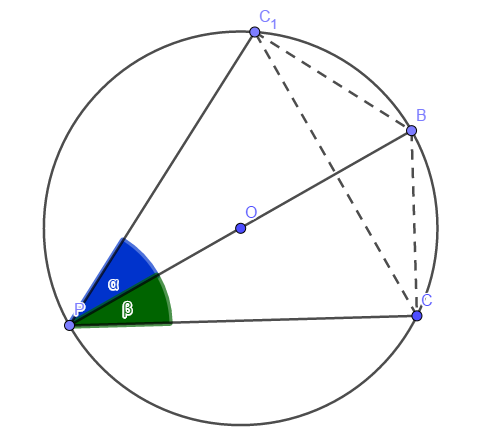
若:
则:四点共圆。
联结,作的外接圆。交射线与点。连。
设的半径为,则:
在圆内接四边形中,根据托勒密定理有:
故:
所以,点和点重合。
因此,点四点共圆。
1 / 2